Parallelograms: Angles
Next, let’s look at properties of the angles in a parallelogram.
|
The first property of angles states that angles opposite each other are congruent. The second property states that consecutive angles, angles that are next to each other, are supplementary. |
Take a look at this figure:
|
If we know that this is a parallelogram, we know the following: • Angle A and Angle C are congruent ( • Angle B and angle D are congruent ( If we know that this is a parallelogram, the opposite sides are parallel. Thinking back to what we learned about parallel lines and the angles that are made when cut by a transversal, we know the following: • Angle A and angle B are supplementary ( • Angle B and angle C are supplementary ( • Angle C and angle D are supplementary ( • Angle A and angle D are supplementary ( |

 )
)  )
)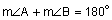 )
) 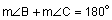 )
) 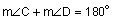 )
) 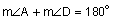 )
)