Perimeter and Area of Parallelograms
You may already be familiar with finding perimeter and area of a parallelogram. Let’s review what you might already know and look at some problems that apply what you have learned in this section.
Perimeter
The perimeter of a parallelogram can be found by adding the lengths of all four sides. This formula can be simplified since we know that each pair of parallel sides is congruent. P equals 2 times side 1 plus 2 times side 2, assuming that side 1 and side 2 are consecutive sides.
Perimeter: P = s1 + s2 + s3 + s4
*This formula can be simplified since we know that each pair of parallel sides is congruent.
|
P = 2s1 + 2s2, assuming that side 1 and side 2 are consecutive sides. |
Example: Find the perimeter of the parallelogram show here.
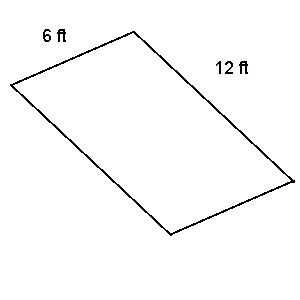
Solution:
Since this is a parallelogram, we know that opposite sides are congruent. We have two sides that at 6 feet and two sides that are 12 feet.
P = 2(6) + 2(12)
P = 36
The perimeter is 36 feet.
Area
|
Area: A = b•h |
*We must be careful here that we use the correct dimensions. The height is the perpendicular distance from one side to the side parallel to it.
Example: Find the area of the parallelogram show here.
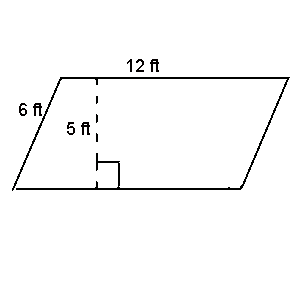
Solution: In this parallelogram, the height is equals to 5 feet. This is the perpendicular distance between the two sides that are equal to 12 feet. A = 12(5) A = 60 The area is 60 square feet.