Section Warm-Up
Section Warm-Up
 Think & Click: Section Warm-Up
Think & Click: Section Warm-Up
Now, you try. Complete the Think & Click activity by looking at the problem below, thinking about it, and then clicking on the question to reveal the solution.
Define parallel lines.
Parallel lines are lines that are coplanar and never cross.
Angle A and angle B are supplementary. Angle A measures (3x + 5)° and angle B measures (2x – 10)°. Find the measure of each angle.
(3x + 5) + (2x – 10) = 180
x = 37
insert image: measure of angle A = [3(37) + 5]° = 116°
insert image: measure of angle B= [2(37) – 10]° = 64°
Solve this system of equations:
8x + 9y + 4x + 15 = 180
10y + 5 = 4x + 15
8x + 9y + 4x + 15 = 180
10y + 5 = 4x + 15
12x + 9y = 165
3(-4x + 10y = 10)
12x + 9y = 165
-12x + 30y = 30
39y = 195
y = 5
12x + 9(5) = 165
12x = 120
x = 10
x = 10, y = 5
3(-4x + 10y = 10)
12x + 9y = 165
-12x + 30y = 30
39y = 195
y = 5
12x + 9(5) = 165
12x = 120
x = 10
x = 10, y = 5
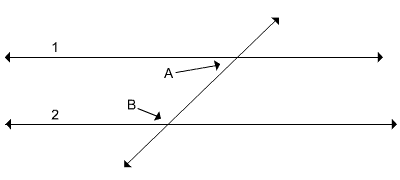
If lines 1 and 2 are parallel, what can you say about angle A and angle B?
Angle A and angle B are supplementary; they add up to 180°.
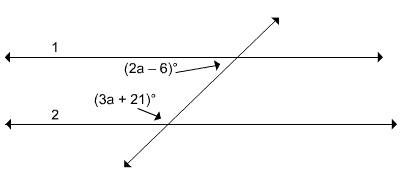
If line 1 and 2 are parallel, find the value of a.
(2a – 6) + (3a + 21) = 180
a = 33