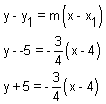Point-Slope Form
Depending on the given information, it can be useful to write the point-slope form of an equation. When you are given one point and the slope, this is the easiest form to use.
|
Example 1
Write the equation of the line through (4, -5) with a slope of 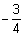 .
.
Simply substitute the given information into the given equation.
You can also use the point-slope form of an equation to help you to write the slope-intercept form of an equation.
Example 2
Write the equation of the line through (1, 2) and with a slope of -3 in slope-intercept form.
First, write the equation in point-slope form.
y - 2 = -3(x - 1)
Now, solve the equation for y.
y - 2 = -3(x - 1)
Apply the distributive property.
y - 2 = -3x + 3
y = -3x + 5
The equation is now in slope-intercept form.