Perpendicular Lines

If the product of the slopes of two lines is −1, then they are perpendicular.

For example, y = −3x + 11 is perpendicular to y = 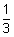x + 12 and y = −x + 4 is perpendicular to y = x − 6, because

(−3)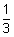 = −1 and (−1)(1) = −1.

When two slopes multiply to −1, we say that the slopes are negative reciprocals of one another.

If a line has a slope of 4, the perpendicular slope is .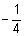

If the slope has a slope of 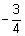then perpendicular slope is .

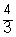Comparing perpendicular lines, one slope is positive and the other is negative; both cannot be positive and both cannot be negative.

Example 1

Write the equation of the line perpendicular to y = 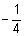x + 7 that passes through the point (2, −5) in slope−intercept form.

Since the slope of our original equation is 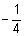, the slope of our new equation will be the negative reciprocal or 4.

First write the equation in point-slope form.

y + 5 = 4(x − 2)

Then convert the equation to slope-intercept form.

y + 5 = 4x − 8

y = 4x − 13

Example 2

Determine if the two lines are perpendicular.

Line 1: 5x + 10y = 20

Line 2: 8x − 4y = −16

First we have to change line 1 and 2 into the slope intercept form.

Line 1:

5x + 10y = 20

10y = −5x + 20

y = −x + 2        (so the slope is −)

Line 2:

8x − 4y = −16

−4y = −8x − 16

y = 2x + 4             (so the slope is 2)

Now multiply the slope of the first line with the slope of the second.

(−) * 2 = −1

Since the answer is −1 after you multiply, the lines are perpendicular.

Next: Section C, page 12

© 2009 KC Distance Learning. All rights reserved.