Conic Sections: Ellipses

Graphing an Ellipse With a Center at (h, k)

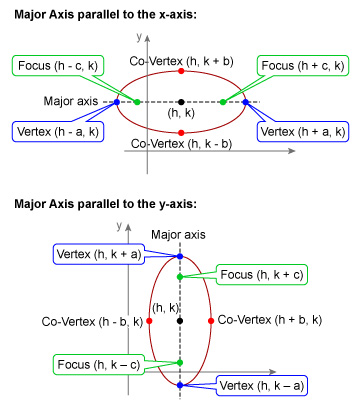
Like circles, ellipses do not need to be centered at the origin, they can be centered at a point (h, k). The following are the standard equations of an ellipse that either has a horizontal or vertical major axis.

Equation Center Major Axis Foci Vertices Co-Vertices
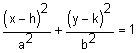x minus h quantity squared divided by a squared plus y minus k quantity squared divided by b squared equals 1

a2 > b2 and a2 – b2 = c2		 (h, k) Parallel to the
x-axis, horizontal		 (h-c, k)
(h+c, k)		 (h-a, k)
(h+a, k)		 (h, k-b)
(h, k+b)
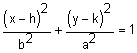x minus h quantity squared divided by b squared plus y minus k quantity squared divided by a squared equals 1

a2 > b2 and a2 – b2 = c2		 (h, k) Parallel to the
y-axis, vertical		 (h, k-c)
(h, k+c)		 (h, k-a)
(h, k+a)		 (h-b, k)
(h+b, k)

The first ellipse has the following characteristics: focus at h minus c, k; focus at h plus c, k; vertex at h minus a, k; vertex at h plus a, k; co-vertex at h, k plus b; co-vertex at h, k minus h; center h, k; horizontal major axis. The second ellipse has the following characteristics: focus at h plus c, k; focus at h minus c, k; vertex h plus a, k; vertex h plus a, k; co-vertex h minus b, k; co-vertex h plus b, k; center h, k; and vertical major axis.