Conic Sections: Ellipses

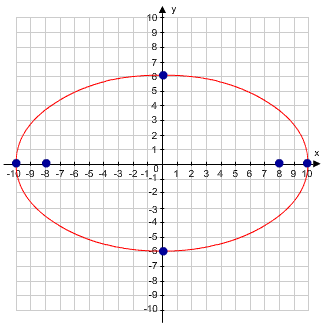
Example of an Ellipse with a Center at the Origin

Suppose you are asked to graph the ellipse 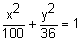x squared divided by 100 plus y squared divided by 36 equals 1. The first step is to identify a, b, and c.

a = 10
b = 6
square root of the quantity 100 minus 36 equals square root of 64 equals 8

This means the foci are at (-c, 0) and (c, 0) or (-8, 0) and (8, 0). The major axis has a length of 2a or 20 and the minor axis has a length of 2b or 12. The vertices are at (-10, 0) and (10, 0) and the co-vertices are at (0, -6) and (0, 6). We are now ready to draw the graph. You should label your major and minor axes and then your vertices and co-vertices. Then you can draw the general shape of the ellipse.

Graph of x squared over one hundred plus y squared over thirty six is equal to one