Graphing an Ellipse with a Center at the Origin
As with circles, ellipses have a center. We will start our discussion by talking about those ellipses that have a center at the origin.
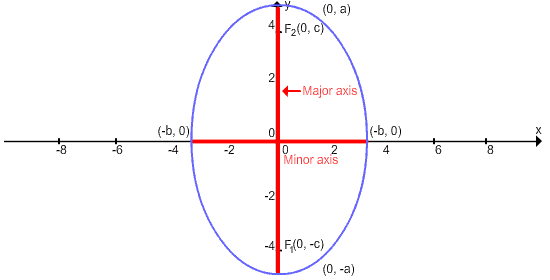
An ellipse has two axes of symmetry. The major axis is the longer axis of the ellipse and the minor axis is the shorter axis of the ellipse. The endpoints of the major axis are called the vertices and the endpoints of the minor axis are called the co-vertices.
The standard equation of an ellipse that is centered at the origin has either a horizontal or a vertical major axis.
Horizontal Major Axis
, where a2 > b2 and a2 – b2 = c2
The length of the major axis is 2a.
The length of the minor axis is 2b.

Vertical Major Axis
, where a2 > b2 and a2 – b2 = c2
The length of the major axis is 2a.
The length of the minor axis is 2b.