Distance Formula
We will begin our discussion of conic sections by reviewing the Distance Formula and the Midpoint Formula.
Conic sections can be studied as figures on a coordinate plane. They can be described in terms of the distances between points. This is why the distance formula is an integral part in the study of conic sections.
Analyze the following diagram.
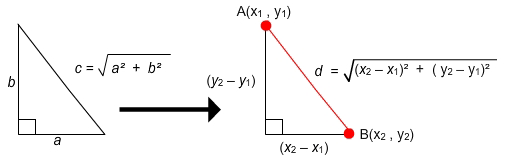
On the left you have a triangle with sides a, b, and c. Side c is the hypotenuse and is equal to ![]() .
.
On the right you have the same triangle with points A and B defined. A has coordinate (x1, y1) and B has coordinate (x2, y2).
Using the Pythagorean Theorem again we can find side d, which is the distance between points A and B.
This is the definition of the distance between two points.
