Conic Sections: Introduction to Conic Sections

Circles

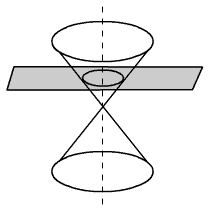
Double-napped cone cut by a plane to produce a circle

The two cones shown in the above image are called double-napped right circular cones. A plane that cuts one nappe completely and is perpendicular to the axis of the cone creates a circle.

A circle is the set of all points in a plane that are a constant distance, called the radius, from a fixed point, called the center.

The standard equation of a circle is given by the equation

x2 + y2 = r2

This circle has a center at (0, 0) and a radius of r.

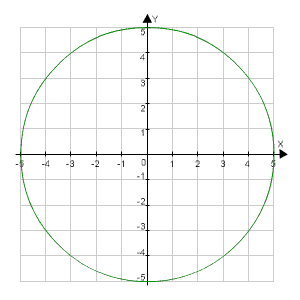
For example, the following is the graph of circle x2 + y2 = 25.

Graph of x squared plus y squared equals twenty five

This is a circle with a center at (0, 0) and a radius of 5 since r2 = 25.