Parabolas

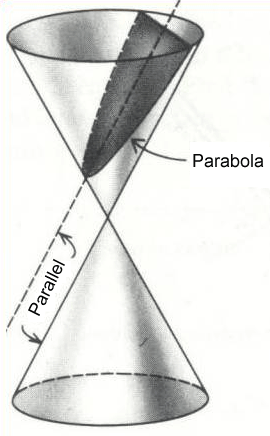
If the plane doesn't cut across one entire nappe or intersect both nappes, the curve of the intersection is called a parabola. A parabola is the set of all points P(x, y) in the plane whose distance to a fixed point, called the focus, equals its distance to a fixed line called the directrix.

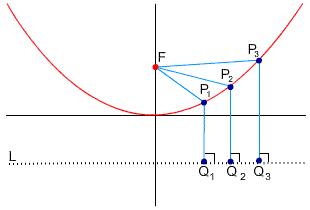
In this figure L is the directrix and F is the focus. By the definition of a parabola, 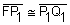, , 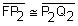and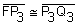

The equation of a parabola with a vertex at the origin falls under one of the following two categories.

Horizontal Directrix

The value of p is the distance from the focus to the vertex. When p > 0 the parabola opens upward. When p < 0 the parabola opens downward.

Vertical Directrix

The value of p is the distance from the focus to the vertex. When p > 0 the parabola opens to the right. When p < 0 the parabola opens to the left.