Conic Sections: Introduction to Conic Sections

Hyperbola

Double-napped cone cut by a plane to produce a hyperbola

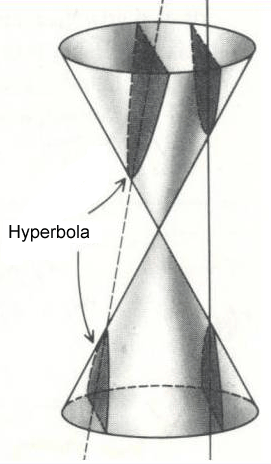
If the plane cuts through both nappes of the cone, the curve is called a hyperbola.

A hyperbola is the set of points P(x, y) in a plane such that the absolute value of the difference between the distances from P to two fixed points in the plane, F1 and F2, called the foci, is a constant.

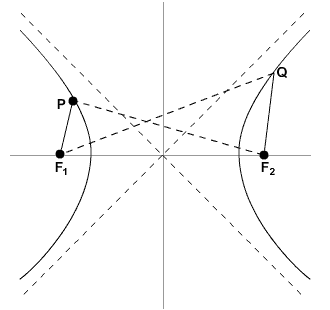
Hyperbola centered at the origin opening to the left and right, with focus F 1 to the left and F 2 to the right.

The hyperbola has two axes of symmetry. One axis contains the transverse axis and the other contains the conjugate axis.

A2_8_1_13_GraphOfHyperbola.gif

In the image above, "a" is defined as the distance from the center to the endpoint of the transverse axis; "b" is the distance from the center to the endpoint of the conjugate axis.

The standard equation of a hyperbola falls into the following two categories.

Horizontal Transverse Axis

x squared divided by a squared minus y squared divided by b squared equals 1

Vertical Transverse Axis

y squared divided by a squared minus x squared divided by b squared equals 1