Conic Sections: Introduction to Conic Sections

Ellipses

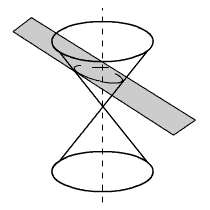
Double-napped cone cut by a plane to produce an ellipse

If the plane isn't perpendicular to the axis of the cone but it crosses the whole nappe, it is called an ellipse.

Ellipse with a point P on the curve and foci F one and F two, r 1 is the distance from F 1 to P and r 2 is the distance from F 2 to P

In the image above, "a" is defined as the distance from the center to the endpoint of the major axis; "b" is the distance from the center to the endpoint of the minor axis.

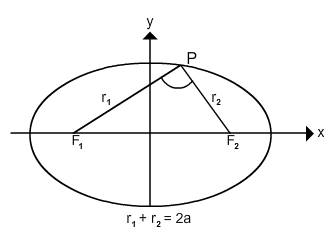
An ellipse is the set of all points P in a plane such that the sum of the distances from P to two fixed points F1 and F2, called the foci, are constant. This means r1 + r2 = 2a.

An ellipse has two axes of symmetry. The major axis is the longer axis of the ellipse and the minor axis is the shorter axis of the ellipse.

The standard equation of an ellipse falls into the following two categories.

Horizontal Major Axis

x squared divided by a squared plus y squared divided by b squared equals 1

Vertical Major Axis

x squared divided by b squared plus y squared divided by a squared equals 1