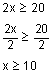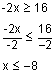Solving Linear Inequalities

Now that we have analyzed the properties of inequalities, we can start to use the properties to solve linear inequalities.

Solve 2x – 3 ≥ 17 and graph the solution on a number line.

The first step is to add 3 to both sides.

2x – 3 + 3 ≥ 17 + 3
2x ≥ 20

The next step is to divide both sides by 2.

Graph this inequality on a number line. The answer involves a greater than or equal to sign, therefore the number 10 is included in the solution. Think back to your warm-up. This means that we draw a closed dot at 10. If the answer involved < or > then we would draw an open dot because the answer did not include the number 10.

Graph of x ≥ 10

Let’s take a look at one more example.

Solve -2x ≥ 16 and graph the solution on a number line.

The first step is to divide both sides by -2. Since we are dividing by a negative number, we will need to switch the direction of the inequality.

Graph of x ≤ -8