Absolute Value Inequalities

Just as we learned to solve linear inequalities, we can solve absolute value inequalities. There are some rules that we use when solving these types of inequalities.

1. If a > 0 and
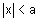
   then x > -a and x < a
    
2. If a > 0 and
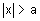
   then x < -a or x > a

The same rules apply for ≥ and ≤.

Let’s see how these rules help us solve absolute value inequalities.

Solve .

Use the rules to write two inequalities. Since we are working with ≥ we will use rule #2.

2x + 1 ≤ -5 or 2x + 1 ≥ 5

Now solve both of the absolute value inequalities.

2x + 1 ≤ -5
2x ≤ -6
x ≤ -3

or

2x + 1 ≥ 5
2x ≥ 4
x ≥ 2

Graph your solution to make sure that it is valid.

Graph of Absolute Value Inequality

Since our two absolute value inequalities are linked with an “or” statement, this graph is valid and our solutions are true.

Next: Section B, page 16

© 2009 KC Distance Learning. All rights reserved.