Properties of Equality
Before we can start solving linear equations it is important to go over the Properties of Equality. Look over the following list:
For real numbers a, b, and c:
Reflexive Property |
a = a |
Symmetric Property |
If a = b, then b = a |
Transitive Property |
If a = b and b = c, then a = c |
Addition Property |
If a = b, then a + c = b + c |
Subtraction Property |
If a = b, then a – c = b – c |
Multiplication Property |
If a = b, then ac = bc |
Division Property |
If a = b, then |
 We are going to be using these properties as we solve linear equations and inequalities. The key to solving linear equations is to think of a balance. If you put something or take something away from one side, you must do the same to the other. For example, look at the Subtraction Property. Notice that c is subtracted from both sides of the equation, to keep the balance even. Let’s call this balance the Algebraic Balance.
We are going to be using these properties as we solve linear equations and inequalities. The key to solving linear equations is to think of a balance. If you put something or take something away from one side, you must do the same to the other. For example, look at the Subtraction Property. Notice that c is subtracted from both sides of the equation, to keep the balance even. Let’s call this balance the Algebraic Balance.
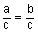 , where c ≠ 0
, where c ≠ 0