Linear and Quadratic Functions: Solving Linear Equations and Inequalities

Absolute Value Examples

Teacher TeachingLet’s work through some examples so that we can better understand how to solve absolute value equations.

  1. Solve the absolute value of x plus 3 equals 5.

First set up your two equations.

x + 3 = 5 or x + 3 = -5

Solving each of the equations we calculate that x = 2 and x = -8.

One important step that you can’t forget is to check your work. You may find that some solutions do not work in the original absolute value equation. In this case, if we plug x = 2 and x = -8 into the absolute value equation, we find both quantities satisfy the equation.

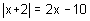  1. Solve the absolute value of x plus 2 equals 2 x minus 10.

First set up your two equations.

x + 2 = 2x – 10 or x + 2 = -(2x – 10)

Solve each of the equations.

x + 2 = 2x – 10
2 = x – 10
x = 12

or

x + 2 = -(2x – 10)
x + 2 = -2x + 10
3x + 2 = 10
3x = 8
x equals eight thirds

Now check both answers in your original equation. You will notice that 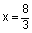x equals eight thirds does not work in the original equation. Therefore, x = 12 is the only answer.

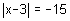  1. Solve the absolute value of x minus 3 equals negative 15.

Take a close look at this absolute value equation. Recall that an absolute value can never be negative. In this case, we are asked to solve a problem that is impossible to solve since the absolute value of x minus 3 equals negative 15 can never happen. Therefore, there is no solution to this problem.