Absolute Value Equations

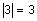Recall from previous courses that the absolute value is defined as the distance from a number on a number line to zero. Since distance can never be negative, neither can the absolute value. Absolute value is denoted by the symbol . If we keep this definition in mind, we find that and 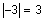since the distance from 3 to zero and -3 to zero on the number line is 3.

You will always be setting up two equations that go along with your absolute value equation. Absolute value equations may have two solutions, no solution, or a solution of All Real Numbers. Let’s concentrate on the two solutions. Why does this make sense? The best way to describe this scenario is to look at a graph of an absolute value function. The following is the graph of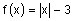

Notice that this graph indicates two solutions where the absolute value function equals zero.