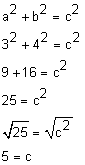Lines and the Coordinate Plane: The Coordinate Plane

Warm-Up Icon Section Warm-Up

In this section, you will learn about points and how to find the distances between them.  In order to do this, you will need the Pythagorean Theorem, which you may have learned about in an earlier math class.

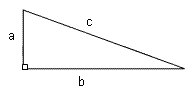
Recall that for right triangles, the Pythagorean Theorem states that the sum of the squares of the legs, a and b, is equal to the square of the hypotenuse, c.

a2 + b2 = c2


Recall that for right triangles, the Pythagorean Theorem states that the sum of the squares of the legs, a and b, is equal to the square of the hypotenuse, c.

a2 + b2 = c2

Example:

Find c.

right triangle with legs 3 and 4 and hypotenuse c

Solution:

a squared plus b squared equals c squared, 3 squared plus 4 squared equals c squared, 9 plus 16 equals c squared, 25 equals c squared the square root of 25 equals the square root of c squared 5 equals c


think icon Think & Click

Now, you try. Complete the Think & Click activity by looking at the problem below, thinking about it, and then clicking on the question to reveal the solution.

Using the triangle below as a reference, solve for c.

right triangle with legs a and b and hypotenuse c

Legs: a = 5, b = 12
 

Hypotenuse: c = 13
 

Legs: a = 7, b = 6
 

Hypotenuse: c = 9.22
 

Legs: a = 8.4, b = 2.7
 

Hypotenuse: c = 8.82