Distance, Position, and Displacement

In the mini-lab you established a working model for an object traveling along a straight line path.

Mathematical Model: Position of Object (Constant Motion)

Before moving on, it is important to distinguish between distance, position, and displacement. There are terms that will help you describe the motion of an object relative to a particular spot. Roll your mouse over the words below to determine the difference between the three important terms when discussing translational (not rotational) motion.

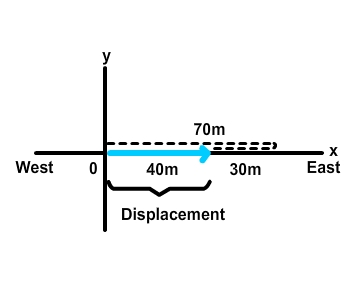
Displacement is a vector quantity—it represents both magnitude (how much) and direction (which way). They are represented by arrows in diagrams.

Let’s take a closer look at the equation you generated in the mini-lab: . In this case, the motion of the car was all in one direction, so distance and displacement are the same, but you will use this equation to describe the displacement of the object, not distance. Remember, displacement is the change in the objects position. You can solve this equation for displacement by subtracting from both sides of the equation:

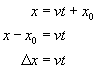
Notice here the delta is used to describe the difference between the final and initial positions. You will see the Greek letter Delta used to describe similar differences—anytime you subtract an initial quantity from a final quantity, you can use the Greek letter Delta.

It is a good idea to begin a variable chart in your notes that you can reference often. Here are the variables you’ve studied so far:

Variable	Meaning
	Final Position
	Initial Position
	Average Velocity
	Time