Kinematics: Motion in One Dimension

New Mathematical Model: Constant Acceleration

For now, since acceleration is constant, the average acceleration and the instantaneous acceleration are the same. The difference between average and instantaneous acceleration can be found on a velocity versus time graph.

Key concept Mathematical Models: Constant Acceleration

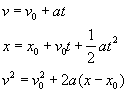
v equals v nought plus a times t; x equals x nought plus v nought times t plus one half times a times t squared; v squared equals v nought squared plus two a times the quantity x minus x nought.

Using the New Model in Problem Solving

Example 1

A sports car accelerates from rest to 95 km/h is 6.2 s. What is its average acceleration in m/s2?

Given: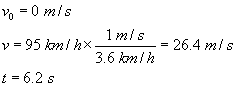
v not equals zero meters per second; v equals ninety five kilometers/hour times one meter per second over three point six kilometers per hour equals twenty six point four meters per second; t equals six point two seconds
Find:
acceleration, a		 Equations:
v equals v nought plus a times t
Solution: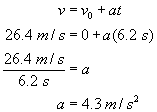
v equals v nought plus a times t; twenty six point four meters per second equals zero plus a times 6.2 seconds; twenty six point four meters per second over six point two equals a; a equals four point 3 meters per seconds squared

Example 2

A world-class sprinter can burst out of the blocks to essentially top speed (of about 11.5 m/s) in the first 15.0 m of the race. What is the average acceleration of the sprinter, and how long does it take her to reach that speed?

Given: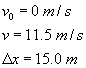
v nought equals zero meters per second; v equals eleven point five meters per second; delta x equals fifteen point zero meters
Find:
acceleration, a
time, t		 Equations:
v squared equals v nought squared plus two a times the quantity x minus x nought

x equals x nought plus v nought times t plus one half times a times t squared
Solution:
Finding acceleration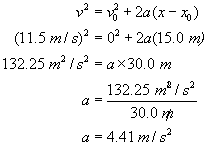

v squared equals v nought squared plus two a times the quantity x minus x nought; the square of eleven point five meters per second equals zero squared plus two times a times fifteen meters; 132.25 meters squared per seconds squared equals a times thirty point zero meters; a equals 132.25 meters squared per seconds squared over thirty point zero meters; a equals four point four one meters per second squared

Finding time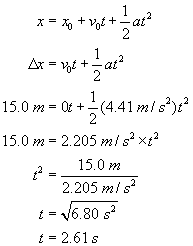

x equals x nought plus v nought times t plus one half times a times t squared; delta x equals v nought times t plus one half times a times t squared; fifteen point zero meters equals zero times t plus one half 4.41 meters per second squared times time squared; fifteen point zero meters equals two point two zero five meters per second squared times t squared; t squared equals fifteen point zero meters over two point two zero five meters per second squared; t equals the square root of six point eight zero seconds squared; t equals two point six one seconds