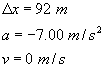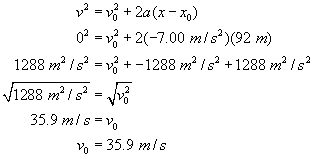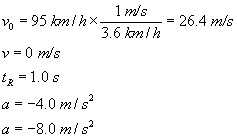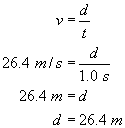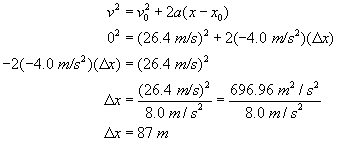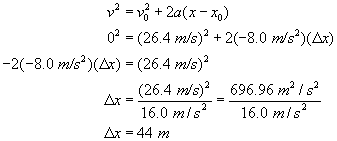Kinematics: Motion in One Dimension

self check Constant Acceleration Self-Check

Now, you try. Complete the self-check activity by looking at the questions below, working them out, and then clicking on the question to review the explanation.

think and click icon
In coming to a stop, a car leaves skid marks 92 m long on the highway. Assuming a deceleration of 7.00 m/s2, estimate the speed of the car just before braking.
Given:
delta x equals ninety two meters; a equals negative seven point zero zero meters per second squared; v equals zero meters per second
Find:
initial speed, v0		 Equations:
v squared equals v nought squared plus two a times the quantity x minus x nought
Solution:
v squared equals v nought squared plus two a times the quantity x minus x nought; zero squared equals v nought squared plus two times negative seven point zero zero meters per second squared times ninety two meters; 1288 meters squared per seconds squared equals v nought squared plus negative 1288 meters squared per second squared plus 1288 meters squared per second squared; square root of 1288 meters squared per second squared equals square root of v nought squared; thirty five point nine meters per second equals v nought; v nought thirty five point nine meters per second.

think and click icon
Determine the stopping distances for a car with an initial speed of 95 km/h and human reaction time of 1.0 s, for an acceleration of (a) a equals negative four point zero meters per second squared. and (b) a equals negative eight point zero meters per second squared..
Given:
v nought ninety five kilometers per hour times 1 meter per second over three point six kilometers per hour equals twenty point six point four meters per second; v equals zero meters per second; t subscript R equals one point zero seconds; a equals negative four point zero meters per second squared; a equals negative eight point zero meters per second squared
Find:
stopping distances (distance traveled during first second plus delta x of accelerations)		 Equations:
v equals delta x over delta t

v squared equals v nought squared plus 2 a times the quantity x minus x nought
Solution:
Solve first for the distance the car travels during the 1.0 s before hitting the brakes.

v equals d over t; twenty six point four meters per second equals d over one point zero seconds; twenty six point four meters equals d; d equals twenty six point four meters.

Then solve for the stopping distance during the acceleration and add to the distance above.

(a) first acceleration

v squared equals v nought squared plus 2 a times the quantity x minus x nought; zero squared equals the quantity of twenty six point four meters per second end quantity squared plus two times negative four point zero meters per second squared times delta x ; negative two times negative four point zero meters per second squared times delta x equals the quantity of twenty six point four meters per second end quantity squared; Delta x equals the quantity of twenty six point four meters per second end quantity squared over eight point zero meters per second squared equals six hundred ninety six point nine six meters squared per seconds squared over eight point zero meters per seconds squared; delta x equals eighty seven meters.


Thus, the total stopping distance is 26.4 + 87 = 113.4 = 113 m.

(b) second acceleration

v squared equals v nought squared plus 2 a times the quantity x minus x nought; zero squared equals the quantity of twenty six point four meters per second end quantity squared plus two times negative eight point zero meters per second squared times delta x; negative two times negative eight point zero meters per second squared times delta x equals the quantity of twenty six point four meters per second end quantity squared; Delta x equals the quantity of twenty six point four meters per second end quantity squared over sixteen point zero meters per second squared equals six hundred ninety six point nine six meters squared per seconds squared over sixteen meters per second squared; delta x equals forty four meters.


Thus, the total stopping distance is 26.4 + 44 = 70.4 m = 70 m.