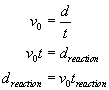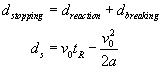Kinematics: Motion in One Dimension

self checkMore Complicated Constant Acceleration Self Check

This question is a little more complicated. Try to figure it out through the manipulation of equations and see if you can find the answer. Note, you’re not finished until you actually prove the answer. Click on the question for the solution (but try it first).

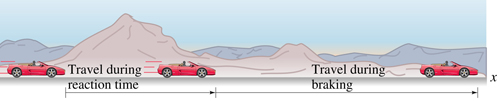
A car accelerating and then braking

think and click icon
Show that the equation for the stopping distance of a car is d subscript s equals v nought times t subscript R minus v nought squared over 2 a, where vO is the initial speed of the car, tR is the driver’s reaction time, and a is the constant acceleration.
We know that the distance covered before breaking (dreactions) can be found using the distance equation:

v nought equals d over t; v nought times t equals d reaction; d reaction equals v nought times t reaction

We also know that the distance covered after breaking (dbreaking) can be found using the velocity equation for constant acceleration:

v squared equals v nought squared plus 2 a times delta x; v squared equals v nought squared plus 2 a times d breaking; zero squared minus v nought squared equals v nought squared plus 2 a times d breaking minus v nought squared; negative of v nought squared over two a equals 2 a times d breaking over 2a; d breaking equals negative of v nought squared over two a

Knowing that the stopping distance takes into consideration both the reaction distance and the breaking distance, we have:

d stopping equals d reaction plus d breaking; d subscript s equals v nought times t subscript R minus v nought squared over 2 a. Notice d stopping became d subscript s and d reaction became d subscript R