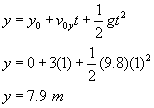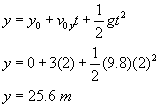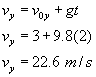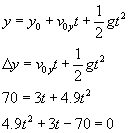Kinematics: Motion in One Dimension

self check Free Fall Problem Solving Self-Check

Let’s look at the more difficult problems dealing with free fall—objects thrown with an initial velocity. Try to work these out, and then click on the question to review the explanation.

Initial downward velocity

Suppose a ball is thrown downward from a 70-m tall tower at 3.00 m/s.

think and click icon
What is the ball’s position after 1.0 second? 2.0 seconds?
Using the equation : y equals y nought plus v nought sub y times t plus one half g times t squared, substitute the correct values in and solve for position. Use +y as the downward direction and the top of the tower as the 0 reference point in terms of position.

 

1 second 2 second
y equals y nought plus v nought sub y times t plus one half g times t squared; y equals zero plus three times one plus one half of nine point eight times one squared; y equals seven point nine meters y equals y nought plus v nought sub y times t plus one half g times t squared; y equals zero plus three times two plus one half of nine point eight times two squared; y equals twenty five point 6 meters

think and click icon
What is the ball’s velocity after 1.0 second? 2.0 seconds?
Using the equation for velocity v = vO + gt, substitute the correct values in and solve for velocity.

 

1 second 2 second
v sub y equals v nought sub y plus g times t; v sub y equals three plus nine point eight times one; v sub y equals twelve point eight meters per second. v sub y equals v nought sub y plus g times t; v sub y equals three plus nine point eight times two; v sub y equals twenty two point six meters per second.

think and click icon
How long will it take the ball to reach the ground?
For time, we must use the position equation y equals y nought plus v nought sub y times t plus one half g times t squared again. You need to make sure your "assumptions" are consistent in your problem solving, so keep the +y as the downward direction and the top of the tower as the 0 reference point in terms of position.

y equals y nought plus v nought sub y times t plus one half g times t squared; delta y equals v nought sub y times t plus one half g times t squared; seventy equals three t plus four point nine t squared; four point nine t squared plus three t minus seventy equals zero

Notice here you will have TWO solutions. Use your knowledge of solving quadratics for roots to solve. The roots of the equation are 3.49 and –4.10. Since time cannot be negative, the only logical answer is 3.49 seconds.

Text book coverFor more practice, solve the following problems from “Chapter 2, Problems” at the end of the chapter. The answers are in the back of your book.

Problems # 33, 35, 37, 39, 41 (extra challenge—43, 45, 47)