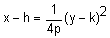Graphing a Parabola with a Vertex (h, k)
If we move the vertex of a parabola away from the origin then we can say the vertex is defined as (h, k). Again, the equation of a parabola with a vertex of (h, k) falls into two categories.
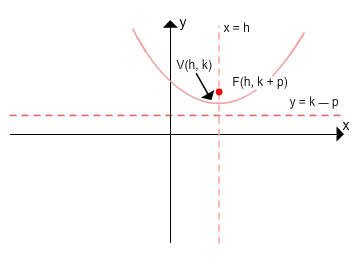
Horizontal Directrix
p > 0: parabola opens upward
p < 0: parabola opens downward
focus: (h, k + p)
directrix: y = k – p
axis of symmetry: x = h
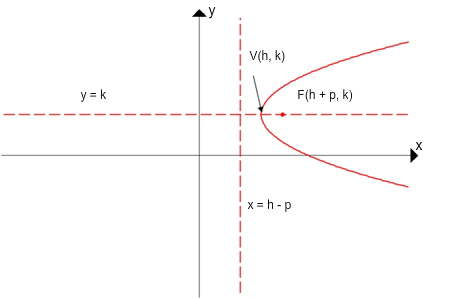
Vertical Directrix
p > 0: parabola opens right
p < 0: parabola opens left
focus: (h + p, k)
directrix: x = h – p
axis of symmetry: y = k