Example: Parabola with a Vertex at the Origin
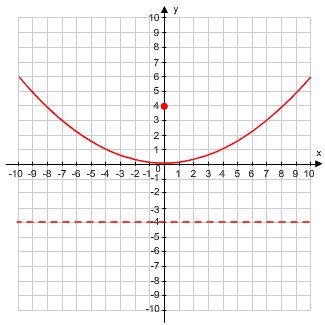
Look below at the graph of 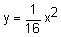 .
.
In this equation p is equal to 4 since we can rewrite 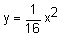 as
as 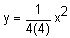 .
.
Since p > 0 the parabola opens upward.
The focus is at (0, p) or (0, 4).
The directrix is defines at y = -p or y = -4.
The axis of symmetry is where the graph can be divided into two symmetrical pieces, both being exactly the same. Notice for this graph this occurs at the y-axis. The axis of symmetry will be very important when we start talking about parabolas with a vertex at a point other than the origin.