Conic Sections: Parabolas

Parabola With a Vertex at the Origin

The first type of parabola that we want to discuss is one whose vertex is at the origin or (0, 0). Remember that a parabola is the set of all points P(x, y) in the plane whose distance to a fixed point, called the focus, equals its distance to a fixed line, called the directrix.

The standard equation of a parabola with a vertex at the origin falls under the following two categories.

Horizontal Directrix

y equals 1 divided by 4 p times x squared

p > 0: parabola opens upward
p < 0: parabola opens downward
focus: (0, p)
directrix: y = -p
axis of symmetry: y-axis

Graph of parabola facing upwards with the focus and directrix labeled. Focus is equal to the point zero comma p. Directrix is the equation y equals negative p.

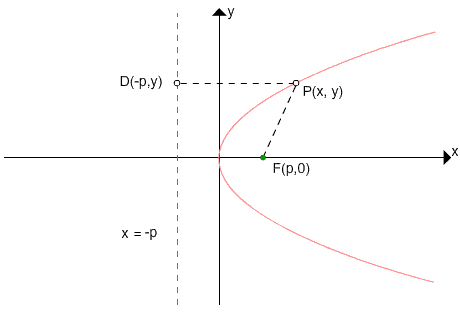
Vertical Directrix

x equals 1 divided by 4 p times y squared

p > 0: parabola opens right
p < 0: parabola opens left
focus: (p, 0)
directrix: x = -p
axis of symmetry: x-axis

Graph of parabola opening to the right with the focus and directrix labeled. Focus is equal to the point p comma zero. Directrix is the equation x equals negative p.