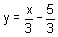Inverse
The next topic we will discuss in our work towards understanding functions and relations is the inverse of a relation. The inverse of a relation consisting of ordered pairs (x, y) is the set of all ordered pairs (y, x). Notice that in order to find the inverse of a relation you interchange the x- and y-values.
For example, if you look at the relation {(-2, 0), (-1, 1), (2, 3), (3, 4)}, the inverse of this relation is {(0, -2), (1, -1), (3, 2), (4, 3)}. You interchange the x- and y-values of the original relation.
What if you are given an equation instead of a set of ordered pairs? The process is the same. You interchange your x- and y-values. Let's look at an example.
Suppose you have the equation y = 3x + 5 and you want to find the inverse of this equation. Here are the steps you need to follow:
- Interchange the x- and y-values in the equation.
x = 3y + 5
- Solve for y.
x = 3y + 5
-3y = -x + 5
3y = x – 5