Linear and Quadratic Functions: Functions and Relations

Relations

Graph of the function f of x equals x to the third power
f(x) = x³

Before we can begin our study of functions, we need to review relations. A relation is a relationship between two variables where the first variable is paired with one or more values of the second variable. This means that a set of x-values is paired with any set of y-values.

The following mapping of ordered pairs is an example of a relation.

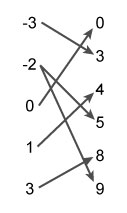
Mapping of negative three to three, negative two to five, negative two to nine, zero to zero, one to four, and three to eight

Mapping of {(-3, 3),
(-2, 5), (-2, 9), (0, 0),
(1, 4), (3, 8)}

You may remember this mapping from your unit warm-up. If we write this mapping out in set notation, we have {(-3, 3), (-2, 5), (-2, 9), (0, 0), (1, 4), (3, 8)}. This is an example of a relation since each of the x-values is mapped to one or more y-values.