Composition of Functions
The last topic that needs to be discussed in terms of functions and relations is the composition of functions. Let f and g be functions of x (f(x) and g(x)). The composition of f and g is written as 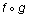 and is defined as f(g(x)).
and is defined as f(g(x)).
One important note. Make sure not to get multiplication confused with composition. This is a commonly made mistake. Composition is denoted with the symbol ![]() while multiplication is denoted with the symbol
while multiplication is denoted with the symbol ![]() .
.
The function 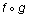 is called the composite function. Let’s see how this works.
is called the composite function. Let’s see how this works.
We are going to work with our two previous functions, f(x) = 2x + 6 and g(x) = 4x – 9.
- Find
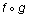 .
.
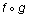 = f(g(x)) = 2(4x – 9) + 6
= f(g(x)) = 2(4x – 9) + 6
g(x) is inserted into the x-value of f(x).
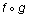 = 8x – 18 + 6
= 8x – 18 + 6
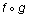 = 8x – 12
= 8x – 12
- Find
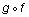 .
.
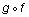 = 4(2x + 6) – 9
= 4(2x + 6) – 9
f(x) is inserted into the x-value of g(x).
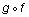 = 8x + 24 – 9
= 8x + 24 – 9
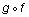 = 8x + 15
= 8x + 15