Functions
How do functions differ from relations? A function is a special kind of relation. A function is a relationship such that each value of the first variable is paired with exactly one value of the second variable. Another way of thinking of the definition of a function is to say that for each x-value there is one and only one y-value.
One easy way to remember the concept of a function is to think of a keyboard on a computer. If you press the "k" key on your keyboard, only the letter "k" appears on your screen. You don’t see the letter "o" or any other letter. The concept is the same for a function. For each value of x, or stroke on the keyboard, only one y-value appears, or one letter on the screen.
The following mapping of ordered pairs represents a function.
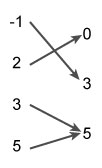
This mapping can be rewritten in set notation, {(-1, 3), (2, 0), (3, 5), (5, 5)}.
Notice that for each value of x there is one and only one y-value. Do not get confused with the ordered pairs (3, 5) and (5, 5). The y-values are the same but the x-values are different. This means that for each x-value there is still one and only one y-value.