Similarity: Similar Polygons

Examples of Perimeter and Area of Similar Polygons

Example 1:
A regular octagon has side lengths equal to 5 feet. The perimeter of this octagon is 40 feet and the area is 120.7 square feet.
A second regular octagon has side lengths equal to 12.5. Find the perimeter and area of the second octagon.

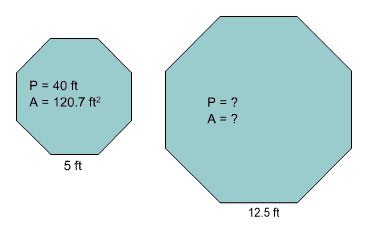Regular Octagon with side lengths 5 feet, perimeter 40 feet and area 120.7 square feet; Regular Octagon with side lengths 12 feet, unknown perimeter and area.

Two Regular Octagons

Solution:
The ratio of the sides of the first octagon to the second octagon is $the fraction 5 over 12 point 5$ .
The ratio of the perimeter of the first octagon to the second octagon is also $the fraction 5 over 12 point 5$ .
$the fraction P sub 1 over P sub 2 equals the fraction 5 over 12 point 5 equals the fraction 40 over P sub 2$

5P₂ = 12.5(40)
5P₂ = 500
P₂ = 100

The perimeter of the second octagon is 100 feet.

The ratio of the area of the first octagon to the second octagon is $the fraction 5 squared over 12 point 5 squared equals the fraction 25 over 156 point 25$
$the fraction A sub 1 over A sub 2 equals the fraction 25 over 156 point 25 equals the fraction 120 point 7 over A sub 2$

25A₂ = 156.25(120.7)
25A₂ = 18,859.375
A₂ = 754.375

The area of the second octagon is 754.375 square feet.

Example 2:
The ratio of the areas of two similar polygons is 25:36. If the perimeter of the first polygon is 25 centimeters, what is the perimeter of the second polygon?

Solution:
If the ratio of the side lengths of similar polygon is A to B, the ratio of the areas is A2 to B2.

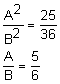
$the fraction A squared over B squared equals twenty-five-thirty-sixths; the fraction A over B equals five-sixths$

The ratio of the side lengths is 5:6, therefore the ratio of the perimeters is also 5:6.

$five-sixths equals the fraction 25 over P sub 2$
5P₂ = 150
P₂ = 30.

The perimeter of the second polygon is 30 centimeters.