Similarity: Similar Polygons

Solving Problems with Similar Polygons

When we know that two polygons are similar, we know that their corresponding angles are congruent and that their corresponding sides are proportional.  Using that information, we can solve problems.

Example:
Given that pentagon ABCDE is similar to pentagon PQRST and given the following information, find the values of w, x, y and z.

Pentagon ABCDE, with angle A equal to 110 degrees, angle B equal to 100 degrees, angle C equal to 99 degrees, angle D equal to 140 degrees and angle E equal to 91 degrees; side AB equal to 3, side BC equal to 5, CD equal to 7, side DE equal to 2 and side EA equal to 6. Pentagon PQRST, with angle P equal to 110 degrees, angle Q equal to 100 degrees, angle R equal to w degrees, angle S equal to 5x plus 20 degrees and angle T equal to 91 degrees; side PQ equal to 4.8, side QR equal to 8, RS equal to y, side ST equal to 2z minus 1 and side TP equal to 9. 6.
Similar pentagons ABCDE and PQRST

 

Solution:
Corresponding angles are congruent.

the measure of angle R equals the measure of angle C, therefore w = 99

the measure of angle S equals the measure of angle D, therefore 5x + 20 = 140
                                               5x = 120
                                               x = 24

Corresponding sides are proportional.

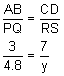
the fraction AB over PQ equals the fraction CD over RS; the fraction 3 over 4 point 8 equals the fraction 7 over y 
3y = 4.8(7)
3y = 33.6
y = 11.2

 

the fraction AB over PQ equals the fraction DE over ST; the fraction 3 over 4 point 8 equals the fraction 2 over the quantity 2 z minus 1 

3(2z – 1) = 4.8(2)
6z – 3 = 9.6
6z = 12.6
z = 2.1