Similar Polygons
If you recall, in the last lesson, we learned that similar triangles have corresponding angles with equal angle measure and corresponding sides that are proportional. We can extend that to polygons with any number of sides.
|
Polygons are similar if:
|
In the previous lesson, it was sufficient to show that all corresponding angles were congruent to show that the triangles are similar. We could also show that corresponding sides were proportional and using the Side-Side-Side Similarity Postulate, we could state that the triangles were similar. Unlike triangles, when working with polygons with more than 3 sides, we must show that the angles are congruent AND the sides are proportional in order to show they are similar polygons.
Take a look at the three trapezoids shown here:
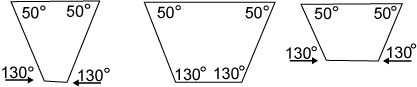 |
Three trapezoids |
It is easy to see that each trapezoid has corresponding angles that are congruent, but the sides of the trapezoids are not proportional. Therefore the trapezoids are not similar.
Take a look at the quadrilaterals shown here:
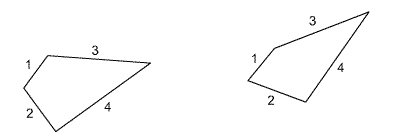 |
Two quadrilaterals |
It is easy to see that each quadrilateral has corresponding sides that are proportional (in this case the ratio is 1:1), but that the angles are not congruent. Therefore the quadrilaterals are not similar.
In order for polygons with more than three sides to be similar, they must have BOTH congruent angles and proportional sides.
Now take a look at the following pair of quadrilaterals.
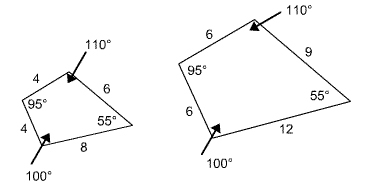 |
SimilarQuadrilaterals |
Notice that all corresponding angles are congruent and corresponding sides are proportional ![]()
Because these polygons have both corresponding angles that are congruent and corresponding sides that are proportional, they are similar.
