Perimeter and Area of Similar Polygons
Let’s look at two similar polygons and compare their perimeters and areas. We will start with basic squares and then find a general rule for all similar polygons.
Take a look at the similar squares below.
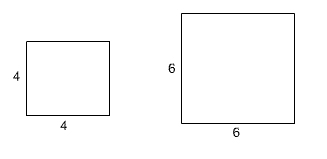 |
Two squares |
The ratio of the side lengths of the first square to the second square is 4:6 or ![]() .
.
The perimeter of each is:
P1 = 4 + 4 + 4 + 4 = 16
P2 = 6 + 6 + 6 + 6 = 24
The ratio of the perimeters is 16:24 or ![]() .
.
Notice that the ratio of the perimeters is the same as the ratio of the sides.
The area of each is:
A1 = 4(4) = 16
A2 = 6(6) = 36
The ratio of the areas is 16:36 or ![]() .
.
Notice that the ratio of the areas is the square of the ratio of the sides.
We can generalize this to all polygons.
|
If the ratio of the sides of two similar polygons is A to B, the ratio of the perimeters is also A to B and the ratio of the areas is A² to B². |
Ratio of sides: ![]()
Ratio of perimeters: ![]()
Ratio of areas: ![]()