Geometric Induction
The following figures are called kites. In a kite, each pair of sides at the end of only one diagonal is equal. For example, in the following kites, each pair of sides at the end of vertical diagonals is equal. Recall that matching hatch marks on individual shapes are congruent. In the figures below, the pairs of sides that are congruent are marked.
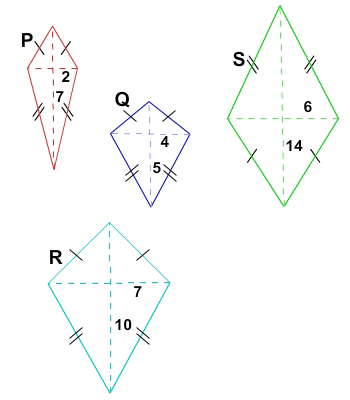
In these kites, the lengths of diagonals are given. Using a computer program, we found the following measures for their areas:
|
Observation 1
|
|
Observation 2 Let's try to develop a pattern using these numbers in terms of the lengths of their diagonals.
We can represent the areas of the kites as a product where one of the factors is one of the diagonals. |
|
Observation 3 Let's try to use the multiplication problems above to find the other diagonal. We can write the second factor in each product as 1/2 of the other diagonal.
|
|
Observation 4 The area of each of these kites is one-half of the product of its diagonals. |
|
Conjecture To find the area of a kite, we simply multiply the diagonals and then find |
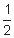 × 2
× 2