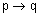Truth and Biconditional Statements
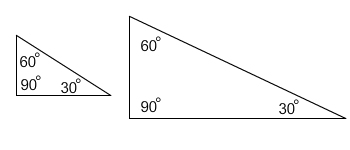
Sometimes the converse of a statement is true and sometimes it is not. In the previous example, "if the corresponding angles of two triangles are congruent, then the triangles are congruent" is not always true. You’ll learn about this when you study triangles, but for now, look at the diagrams.
| If the converse of a true statement is also true, we can write a biconditional statement. A biconditional statement is a conjunction of a conditional and its converse, in which both statements are true. |
Definitions are biconditional statements.
Consider:
"If a number is even, then it is divisible by 2"
p: a number is even
q: it is divisible by 2
The converse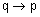 
is also true, if a number is divisible by 2, then it is even.
We can write the biconditional statement as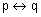 
to show that it is true either way. It doesn’t matter which letter you write first in these cases.
In words we use the phrase "if and only if", often abbreviated "iff", to show that the statement is biconditional:
"A number is divisible by 2 if and only if a number is even."
Remember, a statement must ALWAYS be true both ways to be a biconditional statement. If there is another possible conclusion for the hypothesis, then a biconditional statement is not appropriate for the situation.
