The Law of Detachment and the Law of Syllogism

Earlier in this section, you learned about deductive reasoning.  There are two laws that use deductive reasoning in geometry.

Example:

We are given the following true statement:

p q If two angles are supplementary, then their sum is 180 degrees.

The Law of Detachment follows a pattern like many other applications in mathematics. Here is a helpful pattern to follow:

1. p q
2. p
3. q

For the Law of Detachment to be valid the first statement must be a conditional. It may not be in 'if-then' form. The next statement will refer to the hypothesis ( ) and the final statement will refer to the conclusion ( ).

Below is an example:

If two angles are vertical, then they are congruent (p q).

ABC and DBE are vertical (refers to p).

So, ABC and DBE are congruent (refers to q).

Therefore the argument is valid by the Law of Detachment.

A non-mathematical example of this would be:

If a person is a student, then they ride the bus. 
If I know of a specific student named Billy, I can then apply the general statement to my specific case of Billy and conclude that Billy rides the bus. 

Example:

We are given the following true statements:

If triangles KGC and EHB are similar, then triangles EHB and AFD are similar.

If triangles EHB and AFD are similar, then triangles KGC and AFD are similar.

Draw a conclusion using the Law of Syllogism.

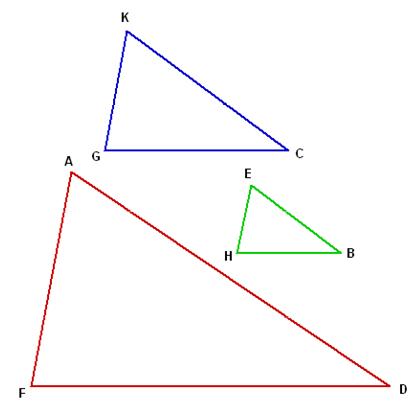
Denote the components of the given statements as follows:

p: Triangles KGC and EHB are similar
q: Triangles EHB and AFD are similar
r: Triangles KGC and AFD are similar

Then, the given true statements can be presented as

p q

q r

Since both these statements are true, using the Syllogism Law, we conclude that
p r. That is, if triangles KGC and EHB are similar, then triangles KGC and AFD are similar.

What conclusion can you draw given the following pair of true statements? Line AB is parallel to line CD Line CD is parallel to line EF           Line AB is parallel to line EF