Introduction to Geometry: Parallel and Perpendicular Lines

Vertical Angles

When angles are across from one another in an X pattern, they are called vertical angles.

In the figure below, angle M L N and angle P L Q are vertical angles. Likewise, angle M L P and angle Q L N are vertical angles.

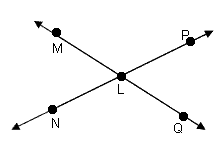
lines M Q and P N intersect at point L

Theorem
Vertical angles are congruent.


This means that angle M L N is congruent to angle P L Q and angle M L P is congruent to angle Q L N.

Why is this true?  In geometry, we can show that something is true by going through a process called proof.  You will learn more about proofs in a later section.  Below is a proof for the theorem above.

Justification
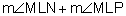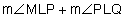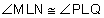measure of angle M L N plus measure of angle M L P= 180° because they are supplementary. Similarly, measure of angle M L P plus measure of angle P L Q= 180°. Setting the left sides of each equation equal to one another and subtracting the measure of angle MLP, we see that measure of angle M L N equals measure of angle P L Q. Thus, angle M L N is congruent to angle P L Q. The other pair of vertical angles can be proved congruent by the same method.