Parallel Line Theorems
Read the following five postulates on parallel lines. To better understand each, click on it and read the example given.
If a line is parallel to one of a set of parallel lines, then it is parallel to all those lines.
In the figure below, lines SR, EF, ED and AB are all known to be parallel. If line MN is parallel to any one of these, it is parallel to all of them.

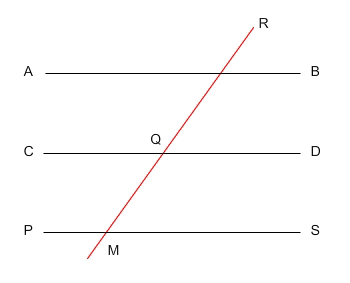
If a transversal intersects one of a set of parallel lines, then it intersects all the other lines.
In the figure below, lines AB, CD and PS are all parallel. Line RQ intersects one line, and therefore, intersects all lines.
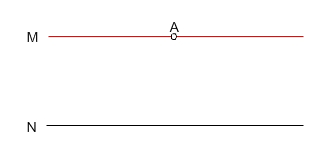
From a point not on a line, one and only one line can be drawn parallel to the given line.
In the figure below, point a does not lie on line N. There is one and only one line that can be drawn parallel to line N through point A. this line is line M.
If two or more lines are perpendicular to a set of parallel lines, then they are parallel.
In the figure below, lines PD and MN are parallel. Line BC is perpendicular to both of these lines. Line QA is also perpendicular to both of these lines. By this postulate, we can state that line BC and line QA are parallel to each other.

If two lines are perpendicular to a pair of parallel lines, the intercepted parts of the perpendicular lines are equal.
In the figure below, lines AB and CD are parallel. Lines MN and PQ are perpendicular to these two lines. By this postulate, the lengths of segments RK and SL are equal.
