 Think & Click: Equation of a Hyperbola
Think & Click: Equation of a Hyperbola
Now, you try. Complete the Think & Click activity by looking at each problem below, thinking about it, and then clicking on the question to reveal the solution.
What is the equation of a hyperbola with vertices at (0, 3) and (0, -3) and co-vertices at (6, 0) and (-6, 0)?
Center: (0, 0).
Vertices: (0, a) and (0, -a), so a = 3.
Co-vertices: (b, 0) and (-b, 0), so b = 6.
Vertical hyperbola: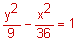
Vertices: (0, a) and (0, -a), so a = 3.
Co-vertices: (b, 0) and (-b, 0), so b = 6.
Vertical hyperbola:
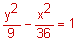
What is the equation of the hyperbola with foci at (8, 0) and (-8, 0) and co-vertices at (0, 2) and (0, -2)?
Center: (0, 0)
Foci: (c, 0) and (-c, 0), so c = 8.
Co-vertices: (0, b) and (0, -b), so b = 2.
a2 + b2 = c2
a2 + 22 = 82
a2 + 4 = 64
a2 = 60
a =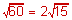
Vertices: (a, 0) and (-a, 0), so (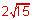 , 0) and (-
, 0) and (-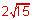 , 0)
, 0)
Horizontal hyperbola:
Foci: (c, 0) and (-c, 0), so c = 8.
Co-vertices: (0, b) and (0, -b), so b = 2.
a2 + b2 = c2
a2 + 22 = 82
a2 + 4 = 64
a2 = 60
a =
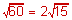
Vertices: (a, 0) and (-a, 0), so (
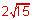 , 0) and (-
, 0) and (-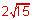 , 0)
, 0)Horizontal hyperbola:

What is the equation of a hyperbola with vertices (7, -3) and (-3, -3) and co-vertices at (2, 3) and (2, -9)?
Center: (2, -3), so h = 2 and k = -3
Vertices: (h + a, k) = (7, -3) and (h – a, k) = (-3, -3). Therefore, a = 5.
Co-vertices: (h, k + b) = (2, 3) and (h, k – b) = (2, -9). Therefore, b = 6.
Horizontal hyperbola:
Vertices: (h + a, k) = (7, -3) and (h – a, k) = (-3, -3). Therefore, a = 5.
Co-vertices: (h, k + b) = (2, 3) and (h, k – b) = (2, -9). Therefore, b = 6.
Horizontal hyperbola:

What is the equation of a hyperbola with foci (-2, 3) and (-2, -5) and co-vertices at (1, -1) and (-5, -1)?
Center: (-2, -1), so h = -2 and k = -1
Foci: (h, k + c) = (-2, 3) and (h, k – c) = (-2, -5). Therefore, c = 4.
Co-vertices: (h + b, k) = (1, -1) and (h – b, k) = (-5, -1). Therefore, b = 3.
Vertical hyperbola: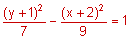
Foci: (h, k + c) = (-2, 3) and (h, k – c) = (-2, -5). Therefore, c = 4.
Co-vertices: (h + b, k) = (1, -1) and (h – b, k) = (-5, -1). Therefore, b = 3.
Vertical hyperbola:
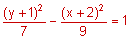
Before continuing, take a moment to practice writing the equation of a hyperbola a little more. Download this worksheet and work through each of the examples.