Conic Sections: Hyperbolas

Graphing a Hyperbola with Center (h, k)

Hyperbolas can have a center that is at point (h, k). Go through the following table that outlines the properties of these types of hyperbolas.

Standard Form of Hyperbola Graph Description
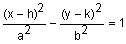x minus h quantity squared divided by a squared minus y minus k quantity squared divided by b squared equals 1

a2 + b2 = c2
2a = length of transverse axis
2b = length of conjugate axis		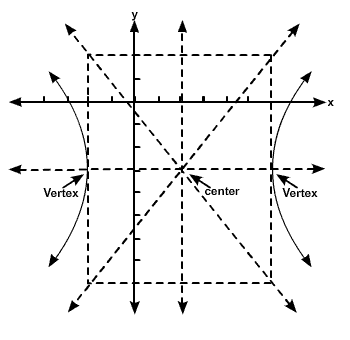 Graph of horizontal hyperbola with center, foci, vertices and co-vertices labeled. center:
(h, k)
foci:
(h ± c, k)
vertices:
(h ± a, k)
co-vertices: (h, k ± b)
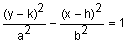y minus k quantity squared divided by a squared minus x minus h quantity squared divided by b squared equals 1

a2 + b2 = c2
2a = length of transverse axis
2b = length of conjugate axis		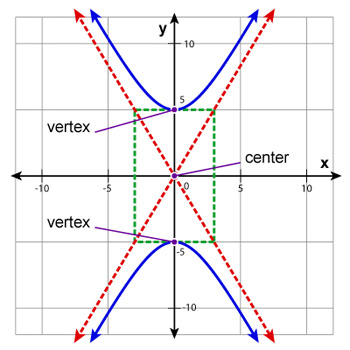 Graph of vertical hyperbola with center, foci, vertices and co-vertices labeled. center:
(h, k)
foci:
(h, k ± c)
vertices: (h, k ± a)
co-vertices:
(h ± b, k)