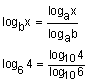Exponential and Logarithmic Functions: Solving Exponential and Logarithmic Equations

Change Of Base Formula

Up to this point we have spent most of our time working with logarithmic functions that are base 10 or a common base. This is not always the case. You may be working with logarithmic functions that are base e, natural log functions or ln, or functions that have a base that is any number other than one. Most calculators will only compute logarithms if they are base 10. There is a formula that allows you to make the change from any base to the common base of 10 or any other base that you want to work with.

Change of Base Formula
For any positive real number a ≠ 1, b ≠ 1, and x > 0,

log base b of x equals the quotient of log base a of x divided by log base a of b

Let's look at an example of how this formula is helpful. Suppose you want to solve the equation
x = log64. You notice that this logarithm has a base of 6 not 10. We can use the change of base formula to solve this equation.

Identify all your variables:

b = 6
x = 4
a = 10 or the base that we want to change into.

log base b of x equals the quotient of log base a of x divided by log base a of b, log base 6 of 4 equals the quotient of log base 10 of 4 divided by log base 10 of 6

Now you can use your calculator to solve the fraction.

log64 ≈ 0.77