Reflections on a Coordinate Axis

Let’s look at reflections on a coordinate axis and see if we can come up with a pattern.

Start with the point (1, 4).  Graph this point on a coordinate axis and then reflect it across the x-axis.  What is the new point?

Reflection through the x-axis

 

As you can see, the new point is (1, - 4).  Notice that the x-coordinate did not change, but the new y-coordinate is the opposite of the original y-coordinate.

Now take the same point (1, 4) and reflect it across the y-axis.  What is the new point?

Reflection across the y-axis

 

As you can see, the new point is (-1, 4).  Notice that the y-coordinate did not change, but the new x-coordinate is the opposite of the original x-coordinate.

Now let’s look at reflecting the point (1, 4) across the line y = x.  What is the new point?

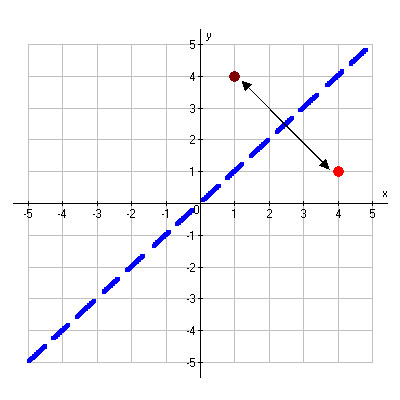Reflection across the line y = x

 

As you can see, the new point is (4, 1).  Notice that the new x- and y-coordinates are the original y- and x-coordinates, respectively.

Let’s look at one last reflection.  Starting with the same point (1, 4), reflect the point across the origin.

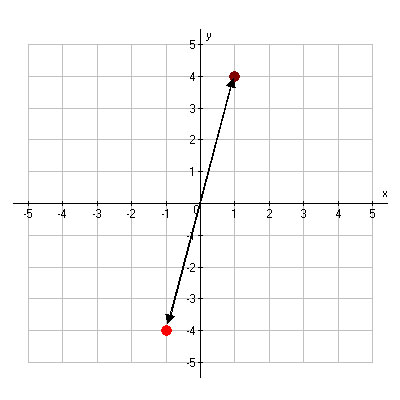Reflection across the origin

 

As you can see, the new point is (-1, -4).  Notice that the new x- and y-coordinates are the opposite of the original x- and y-coordinates.

Summary: Reflection through: Change in x-coordinate Change in y-coordinate x-axis No Change y → -y y-axis x → -x No Change y = x (x, y) → (y, x) origin x → -x y → -y Reflections across the line y = x and through the origin will be important in future math courses.  In this course we are simply studying how to make these transformations.

Next: Section A, page 10

© 2009 KC Distance Learning. All rights reserved.