Translations on a Coordinate Axis
In geometry, we often use a coordinate axis to show specific translations. By using the coordinate axis, we can specify how many units to translate an object, to the left, right, up or down.
To see how this works, let’s look at just one point and the changes in coordinates when translations are performed.
Start with the point (3, 4). Translate it 2 units to the right. What is the new point?
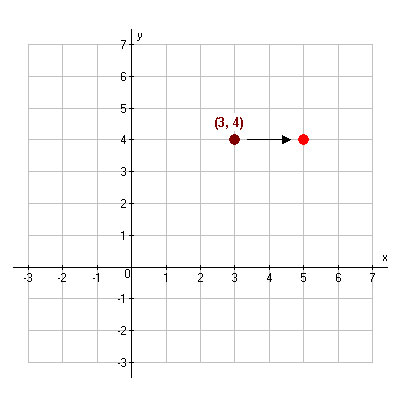 |
(3, 4) Translated 2 Units to the Right |
As you can see, the new point is (5, 4). Notice that the y-coordinate did not change, but the x-coordinate increased by 2.
Now take the same point (3, 4) and translate it 2 units to the left. What is the new point?
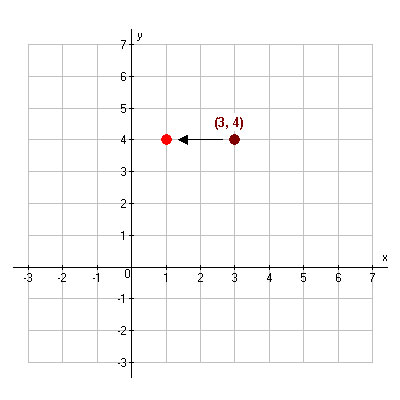 |
(3, 4) Translated 2 Units to the Left |
As you can see, the new point is (1, 4). Notice that the y-coordinate did not change, but the x-coordinate decreased by 2.
Now let’s look at translating the point (3, 4) up and down. Translate the point up 2 units. Then, from the original position of the point, translate it down 2 units. What are the new points?
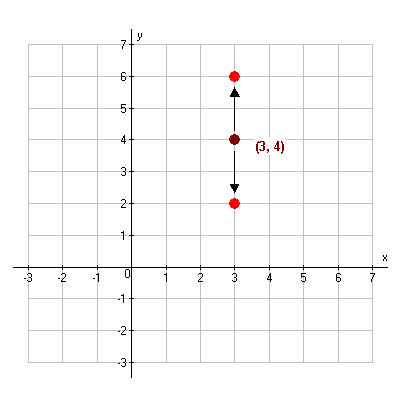 |
(3, 4) Translated 2 Units Up and 2 Units Down |
As you can see, when the point is translated up 2 units the new point is (3, 6). Notice that the x-coordinate did not change, but the y-coordinate increased by 2.
When the point is translated down 2 units the new point is (3, 2). Notice that the x-coordinate did not change, but the y-coordinate decreased by 2.
|
Summary:
|