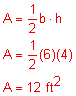Section Warm-Up
In this section, you will be asked to use some geometry skills that you previously learned. Let’s practice these skills before we start applying them to more difficult problems.
Think & Click: Section Warm-Up
Complete the Think & Click activity by looking at each problem below, thinking about it, and then clicking on the question to reveal the solution.
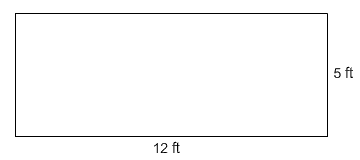
1. Find the perimeter and area of the rectangle below. Be sure to label your answers appropriately.
 |
Rectangle |
P = 2L + 2W
P = 2(12) + 2(5)
P = 34 ft
A = LW
A = (12)(5)
A = 60 ft²
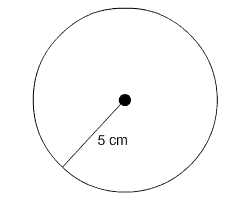
2. Find the circumference and area of the circle below. Be sure to label your answers appropriately.
 |
Circle |
C = 2πr
C = 2π(5)
C = 10π cm
A = πr²
A = π(5)²
A = 25π cm²
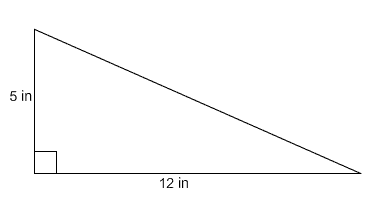
3. Find the perimeter and area of the right triangle below. Be sure to label your answers appropriately.
 |
Right Triangle |
To find the perimeter, we need to know the length of the hypotenuse.
5² + 12² = x²
25 + 144 = x²
169 = x²
13 = x
P = 5 + 12 + 13
P = 30 in
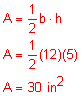
4. Find the perimeter and area of the isosceles triangle below. Be sure to label your answers appropriately.
 |
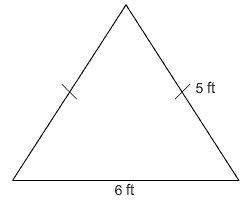Isosceles Triangle |
P = 5 + 5 + 6
P = 16 ft
To find the area, we need to know the height. When the height is drawn, a right triangle is made.
 |
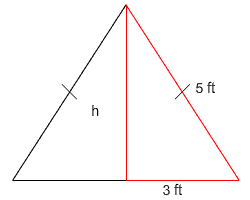Isosceles Triangle |
3² + h² = 5²
9 + h² = 25
h² = 16
h = 4
