Surface Area and Volume: Surface Area and Volume of Prisms and Cylinders

Volume of a Prism

If the three-dimensional figures you have been working with are hollow shapes (like a soup can), each will hold a specific amount of liquid.  This is the concept of volume.

More specifically, volume is the amount of three-dimensional space a figure occupies.  It is the shape’s capacity and measures the cubic units it can hold.

V = (area of base)(height)

 

Volume:

  1. Decide which surfaces are the bases.  Recall that the bases are the same size and shape and are parallel to each other.
  2. Find the area of one of these bases.
  3. Multiply the area of the base times the height of the figure.
  4. Label the answer ‘cubic units’.

Example:
Let’s find the volume of the rectangular prism we first looked at.  Let’s again say it has dimensions L = 10 in, W = 3 in, and H = 4 in.

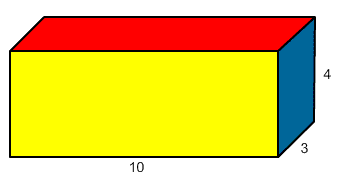Rectangular box with yellow front, red top and blue side, labeled 10 by 3 by 4
Rectangular box

 

1. Decide which surfaces are the bases.  Recall that the bases are the same size and shape and are parallel to each other.

In this case, we have several choices for the bases.  Let’s use the red rectangle on the top and bottom.

2. Find the area of one of these bases.

Area of red base = 10(3) = 30

3. Multiply the area of the base times the height of the figure.

The height of this figure between the red bases is 4.

V = (area of base)(height) = (30)(4) = 120

4. Label the answer 'cubic units'.

The volume is 120 cm3.