Right Triangles and Trigonometry: Ratios of Right Triangles

Examples Using Inverse Trigonometric Functions

Let’s do a few examples together.  Be sure to practice using your calculator so you are sure that you know how to enter them and get the right answer.

Example 1:
Solve the cosine of x equals one-fifth 

Solution:
To eliminate the cosine, take the inverse cosine of both sides.

the inverse cosine of the cosine of x equals the inverse cosine of one-fifth 

The cosine and the inverse cosine cancel out and leave us with just ‘x’ on the left side.  We can use our calculators to evaluate the right side.

x equals the inverse cosine of one-fifth approximately equals 78 point 4 6 3 degrees

Example 2:
Find the measure of angle A in the figure below.

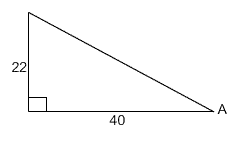
Right triangle with angle A, the side opposite angle A is 22, the side adjacent to angle A is 40

Solution:
The side opposite angle A is 22.
The side adjacent to angle A is 40.
The function that uses the opposite side and the adjacent side is tangent, so we can write the equation:

the tangent of A equals twenty-two-fortieths 

Solve this to find the measure of angle A. Take the inverse tangent of both sides.

the inverse tangent of the tangent of A equals the inverse tangent of twenty-two-fortieths 

The tangent and the inverse tangent cancel out and leave us with just ‘A’ on the left side.  We can use our calculators to evaluate the right side.

A equals the inverse tangent of twenty-two-fortieths approximately equals 28 point 8 1 1 degrees