Right Triangles and Trigonometry: Ratios of Right Triangles

Finding Angles Using Trigonometric Ratios

We will often know side lengths but NOT angles.  We can calculate the angles by setting up the ratios and using our calculators.  You might need to consult your User’s Manual again to see specifically how these are entered on your calculator.

Recall that when you have an equation with multiplication, you use the inverse operation to solve the equation. Division is the inverse of multiplication.  

2x = 10
the quotient 2 x all divided by 2 equals ten-halves 
x = 5

Notice that the multiplying by 2 and the dividing by 2 canceled out to leave us with just ‘x’ on the left side.

Similarly, trigonometric functions have inverses.  They are denoted with an exponent of ‘-1’.

*Note that this exponent of negative 1 looks like a negative 1 power.  It is NOT a power of negative 1.  This is different.  When the negative 1 exponent is used with trigonometric functions, it means inverse.

The inverse of the sine function is ‘sin-1’.
The inverse of the cosine function is ‘cos-1’.
The inverse of the tangent function is ‘tan-1’.

 

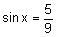
the sine of x equals five-ninths

To solve this, we must ‘eliminate’ the sine on the left side.  We take the inverse sine of both sides.

the inverse sine of the sine of x equals the inverse sine of five-ninths 

Similar to how multiplying by 2 and dividing by 2 cancel out, the sine and the inverse sine cancel out, leaving us with just ‘x’ on the left side.  Our calculators are used to find the value on the right side.

x equals the inverse sine of five-ninths approximately equals 33 point 7 4 9 degrees