Trigonometric Ratios in Real-Life Problems

Now that you understand how to set up the ratios of the six trigonometric functions, you can use them to solve problems.  When a problem is presented to you, use the following steps:

1. Draw a picture representing the problem.
2. Decide which parts of the triangle you will use, based on the information given in the problem.
3. Write an equation using the trigonometric function that fits the information.
4. Solve this equation.

Example 1:
A 15 ft ladder is leaning against a wall.  The ladder is making a 40° angle with the floor.  How far from the wall is the base of the ladder?

Solution:
1. Draw a picture representing the problem.

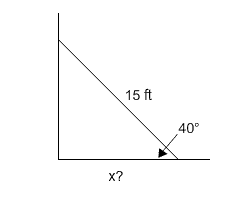Ladder Leaning Against Wall

2. Decide which parts of the triangle you will use, based on the information given in the problem.
The hypotenuse is 15.
The side adjacent to the 40° angle is x.

3. Write an equation using the trigonometric function that fits the information.
Since the cosine uses adjacent and hypotenuse, we can write the equation:
 

4. Solve this equation.
In this case, you can multiply both sides of the equation by 15 to solve for x.
15 cos 40° = x

Using your calculator, find the value of cos 40° (≈ 0.77) and multiply it by 15.
x ≈ 11.49

Example 2:
A 15 ft ladder is leaning against a wall.  The ladder is making a 40° angle with the floor.  How far is the top of the ladder above the ground?

Solution:
1. Draw a picture representing the problem.

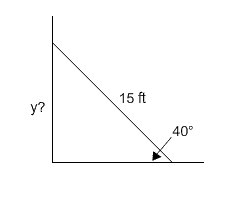Ladder Leaning Against Wall

2. Decide which parts of the triangle you will use, based on the information given in the problem.
The hypotenuse is 15.
The side opposite the 40° angle is y.

3. Write an equation using the trigonometric function that fits the information.
Since the sine uses opposite and hypotenuse, we can write the equation:
 

4. Solve this equation.
In this case, you can multiply both sides of the equation by 15 to solve for y.
15 sin 40° = y

Using your calculator, find the value of sin 40° (≈ 0.64) and multiply it by 15.
y ≈ 9.64